The History of a Science
Hidden in Astronomy Code

Brandon Rhodes
code::dive
Wrocław, Poland
2023 November 16

I’ll talk about:

Skyfield library
History of astronomy
Software design

Skyfield

Open-source
Python using NumPy
Positional astronomy

Positional astronomy is the art
of generating coordinates
for stars and planets

But positional astronomy is
not what most astronomers do!

(Just like most programmers
don’t write compilers)

Normal astronomers:

Get funding
Sign up for observatory time
Then the observatory uses positional
astronomy to compute angles and point
their instrument at the target

So, astronomy libraries for actual
astronomers are mostly ‘science Photoshop’
for the data they get back

Image processing
Spectral analysis
Radio signal processing

But Skyfield’s job is positional astronomy itself:
give it a time, and it will tell you the position
of a star, a planet, or a satellite

A single position is enough to aim a telescope,
while a script that examines a whole series
of positions can answer:

What time does Sun set this evening?
When is the next New Moon?
What month will Jupiter be brightest?
When will the Space Station pass overhead?

—all of which can help
in planning observations.

And, of course, you can also use
coordinates to draw pretty pictures

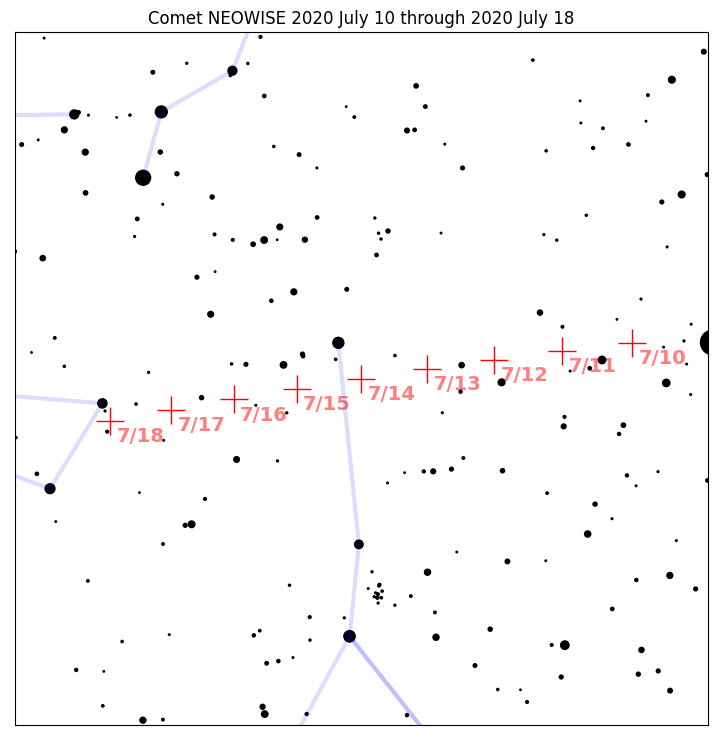
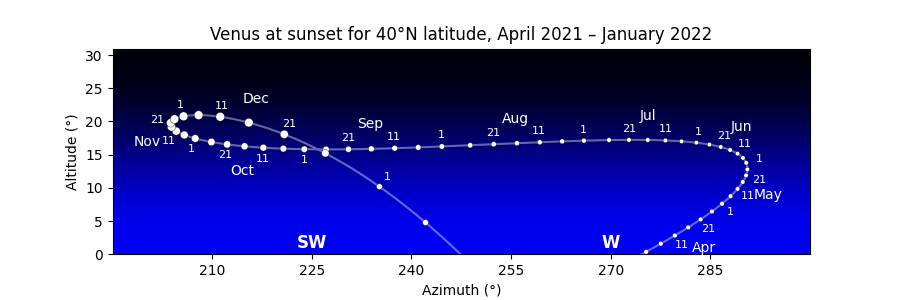
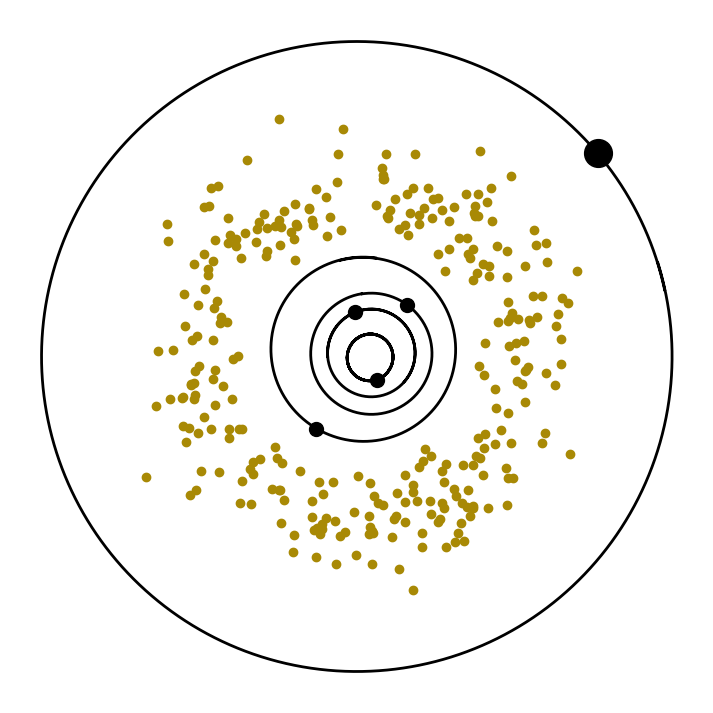
So Skyfield is useful for anyone
who wants to use Python to plan
their own observations

But—how does Skyfield work?

It reads NASA tables
of x,y,z planet positions then
turns those vectors into angles

# Q: Can you just subtract vectors?

jupiter_xyz = jupiter.at(t)
earth_xyz = earth.at(t)
return jupiter_xyz - earth_xyz

#

# Q: Can you just subtract vectors?

jupiter_xyz = jupiter.at(t)
earth_xyz = earth.at(t)
return jupiter_xyz - earth_xyz

# A: No, it takes more work

# Here’s how to generate a position.

def get_position(t, planet):
    earth_xyz, earth_velocity = earth.at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

# This code includes a short history of astronomy!

def get_position(t, planet):
    earth_xyz, earth_velocity = earth.at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

Light-time correction — Ole Rømer (Denmark) 1676

He was observing Jupiter
and its newly discovered moons

                midnight

                   o →


            ↗
 Jupiter  o                 o
                              ↘

─────────────             ─────────────
 morning sky               evening sky

Rømer’s Observation: Jupiter’s moon Io
revolves slightly faster in the morning sky
than it does in the evening sky!

Why would it change speed?

Hypothesis:

Copernicus and Galileo were right, the Earth moves
The Earth moves towards the morning sky
Light takes time to travel

Consequence:

The light-time delay to Jupiter
is getting shorter when Juptier is in the
morning sky and we’re catching up,
so Io looks faster

The light-time delay gets longer again
once we’ve passed Jupiter and left it behind
and it’s fading into the evening sky

As the light-time delay stretches
longer, Io looks slower

‘Light-time correction’

Right now, Jupiter is 33.4 light-minutes away,
so Skyfield needs to use Jupiter’s position from
33.4 minutes ago to generate coordinates

Q:
If you were going to design a unit of measure,
how many units would make a whole?

 1
 2
 3
 4    2
 5
 6    2 3
 7
 8    2 4
 9    3
10    2 5
11
12    2 3 4 6
13
 ⋮   ⋮

 1
 2
 3
 4    2         ←
 5
 6    2 3       ←
 7
 8    2 4
 9    3
10    2 5
11
12    2 3 4 6   ←
13
 ⋮   ⋮

 1
 2
 3
 4    2         ← "highly composite"
 5
 6    2 3       ← "highly composite"
 7
 8    2 4
 9    3
10    2 5
11
12    2 3 4 6   ← "highly composite"
13
 ⋮   ⋮

 1
 2
 3
 4    2
 5
 6    2 3       ← winner all the way to 2×6 = 12
 7
 8    2 4
 9    3
10    2 5
11
12    2 3 4 6   ← winner all the way to 2×12 = 24
13
 ⋮   ⋮

https://oeis.org/A072938

‘Highly composite numbers that are half
of the next highly composite number’

A072938 - A very exclusive club of only 7 numbers

1
2
6
12
60
360
2520

A072938 - Favorites for units of measure

1
2
6
12
60
360
2520

A072938

1
2
6
12   Hours of daylight
60
360
2520

A072938

1
2
6
12   Hours of daylight, Months/year
60
360
2520

A072938

1
2
6
12   Hours of daylight, Months/year
60
360  Degrees in a circle
2520

A question then arose —

An hour is pretty long;
a degree of sky is pretty big;
how should we divide them?

1
2
6
12   Hours of daylight, Months/year
60
360  Degrees in a circle
2520

1
2
6
12   Hours of daylight, Months/year
60   Pars minuta
360  Degrees in a circle
2520

1
2
6
12   Hours of daylight, Months/year
60   Pars minuta prima, pars minuta secunda
360  Degrees in a circle
2520

1
2
6
12   Hours of daylight, Months/year
60   ‘Minute’ and ‘second’
360  Degrees in a circle
2520

1
2
6
12   Hours of daylight, Months/year
60   Pars minuta prima, pars minuta secunda
360  Degrees in a circle
2520

Both times and angles

Hours → 60 minutes → 60 seconds
Degrees → 60 minutes → 60 seconds

Ambiguity?

Hours → 60 minutes → 60 seconds
Degrees → 60 minutes → 60 seconds

‘arc-’

Hours → 60 minutes → 60 seconds
Degrees → 60 arcminutes → 60 arcseconds

12°34′56″

10×50 Binoculars

Jupiter’s moons, star clusters
Craters on the Moon, brighter galaxies
Images right-side-up
Uses both eyes
Portable
569 zł

# So, our `get_position()` function
# is a fun short history of astronomy

def get_position(t, planet):
    earth_xyz, earth_velocity = earth.at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

# But, as code?
# It’s terrible!

def get_position(t, planet):
    earth_xyz, earth_velocity = earth.at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

User
‘How do I ask for astrometric coordinates?’
(that skip aberration and deflection)

#
#

def get_position(t, planet):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)
#

# How can we let the user skip aberration and
# deflection, without breaking existing calls?

def get_position(t, planet):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    xyz = deflect(t, xyz, [sun, jupiter, saturn])
    xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)
#

# Python allows *optional* arguments. Choose
# a default that keeps the *original* behavior!

def get_position(t, planet, apparent=True):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    if apparent:
        xyz = deflect(t, xyz, [sun,jupiter,saturn])
        xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

def get_position(t, planet, apparent=True):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    if apparent:
        xyz = deflect(t, xyz, [sun,jupiter,saturn])
        xyz = aberrate(t, earth_velocity, xyz)
    return xyz_to_coordinates(xyz)

# Let’s add another optional argument.

def get_position(t, planet, apparent=True,
                 angles=True):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    if apparent:
        xyz = deflect(t, xyz, [sun,jupiter,saturn])
        xyz = aberrate(t, earth_velocity, xyz)
    if not angles:
        return xyz
    return xyz_to_coordinates(xyz)

#

def get_position(t, planet, apparent=True,
                 angles=True):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    if apparent:
        xyz = deflect(t, xyz, [sun,jupiter,saturn])
        xyz = aberrate(t, earth_velocity, xyz)
    if not angles:
        return xyz
    return xyz_to_coordinates(xyz)
#

# Another optional parameter.

def get_position(t, planet, apparent=True,
                 angles=True,
                 deflectors=[sun,jupiter,saturn]):
    earth_xyz, earth_velocity = earth_at(t)
    xyz = light_time_correct(t, earth_xyz, planet)
    if apparent:
        xyz = deflect(t, xyz, deflectors)
        xyz = aberrate(t, earth_velocity, xyz)
    if not angles:
        return xyz
    return xyz_to_coordinates(xyz)

# Eventually:

def get_position(
        t, planet, type='apparent', angles=True,
        deflectors=[sun, jupiter, saturn],
        center='Earth', system='ecliptic',
        lat=None, lon=None, elevation=None,
    ):
    ...

# Code becomes littered with `if` statements.
# Hard to test all possible code paths.

# Python Standard Library itself has functions—

s = json.dumps(data)

# —that have obviously gotten caught on the
# Parameter Treadmill:

json.dumps(obj, skipkeys=False, ensure_ascii=True,
           check_circular=True, allow_nan=True,
           cls=None, indent=None, separators=None,
           default=None, sort_keys=False)

Q: So what’s the alternative
to the Parameter Treadmill?

A: LEGO bricks!

LEGO bricks — small interchangeable routines,
which the caller assembles into a solution

# LEGO bricks

from astro import (
    light_time_correct, deflect, aberrate
)

earth_xyz, earth_velocity = earth.at(t)
xyz = light_time_correct(t, earth_xyz, mars)
xyz = deflect(t, xyz, [sun, jupiter, saturn])
xyz = aberrate(t, earth_velocity, xyz)
coordinates = xyz_to_coordinates(xyz)

# Benefit: user has full control!
#
# ‘But I need astrometric coordinates’
# ‘But I need x,y,z coordinates’
# ‘I need to adjust the list of deflectors’

earth_xyz, earth_velocity = earth.at(t)
xyz = light_time_correct(t, earth_xyz, mars)
xyz = deflect(t, xyz, [sun, jupiter, saturn])
xyz = aberrate(t, earth_velocity, xyz)
coordinates = xyz_to_coordinates(xyz)

# Problems:
#
#  • User has to maintain correctness
#  • Library can’t make improvements
#  • Wrong level of abstraction: ‘apparent’?

earth_xyz, earth_velocity = earth.at(t)
xyz = light_time_correct(t, earth_xyz, mars)
xyz = deflect(t, xyz, [sun, jupiter, saturn])
xyz = aberrate(t, earth_velocity, xyz)
coordinates = xyz_to_coordinates(xyz)

Q: Is there a medium?
Parameter Treadmill ← → LEGO bricks

A: Method chaining!

# Method chain


            ┌─ light travel time
            │
            │             ┌─ aberration,deflection
            │             │

earth.at(t).observe(mars).apparent().coordinates()

# Method chain

earth.at(t).observe(mars).apparent().coordinates()

# ‘But I need astrometric coordinates’

earth.at(t).observe(mars).coordinates()

# ‘But I need x,y,z coordinates’

earth.at(t).observe(mars).xyz
earth.at(t).observe(mars).apparent().xyz

# Method chain doesn’t solve everything.

earth.at(t).observe(mars).apparent().xyz

# ‘I need to adjust the list of deflectors’
#
# Well, drat, we still might need a parameter

deflectors = [sun, jupiter, saturn]
earth.at(t).observe(mars).apparent(deflectors).xyz

# But only one!

# Method chain

earth.at(t).observe(mars).apparent().coordinates()

# Benefits:
#  High level of abstraction (‘apparent’)
#  Makes sure methods are called in right order
#  Exposes intermediate results
#  Lets user stop early

The Earth is an oblate spheroid

The centrifugal force of our rotation
makes the Earth’s equator bulge larger
than Earth’s radius at the poles

So an x,y,z vector from Earth’s
center to a city or observatory will have a
different radius depending on latitude

Skyfield at first hard-coded the
standard WGS84 geoid parameters
for turning lat/lon into x,y,z

radius = 6378137.0 m
flattening = 1/298.257223563

# But WGS84’s role was invisible.

wroc = Place(lat=+51.1079, lon=17.0385)

print(wroc.x, wroc.y, wroc.z, 'km')
# -> 3856.2 1399.3 4867.4 km

wroc = Place(lat=+51.1079, lon=17.0385)

# Drat. WGS84 is currently hard-coded,
# there’s no way to specify WGS72.

# Worst idea: global configuration

set_geoid_shape(radius=6378135.0,
                flattening=1/298.26)

wroc = Place(lat=+51.1079, lon=17.0385)

# Problems:
#
#  Invisible action-at-a-distance
#  Ruins thread safety
#  Tightly couples tests

# Slightly better: Parameter Treadmill

wroc = Place(lat=+51.1079, lon=17.0385,
             geoid='wgs72')

# Needs a global registry of geoids

register_earth_geoid(
    'wgs72',
    radius=6378135.0,
    flattening=1/298.26,
)

# Even better: instead of accepting a name,
# accept a Geoid object itself!

wroc = Place(lat=+51.1079, lon=17.0385,
             geoid=wgs72)

# Have the caller simply build and pass in
# their own Geoid struct, and we won’t even
# need a global registry:

wgs72 = Geoid(radius_m=6378135.0,
              flattening=1/298.26)

wroc = Place(lat=+51.1079, lon=17.0385)

print(wroc.x, wroc.y, wroc.z, 'km')
# -> 3856.2 1399.3 4867.4 km

# Then we’re in trouble!  The constructor
# doesn’t accept x,y,z, but insists on
# computing x,y,z itself from lat/lon.

# Best: give Place() a simple x,y,z constructor

kraków = Place(x=3856.2, y=1399.3, z=4867.4)

# Then, give the Geoid class a method
# that builds a Place from a lat/lon

wroc = wgs72.latlon(+51.1079, 17.0385)
wroc = wgs84.latlon(+51.1079, 17.0385)

# The geoid= parameter disappears!
# We’ve escaped the Parameter Treadmill!
# Choice of geoid is now always explicit!

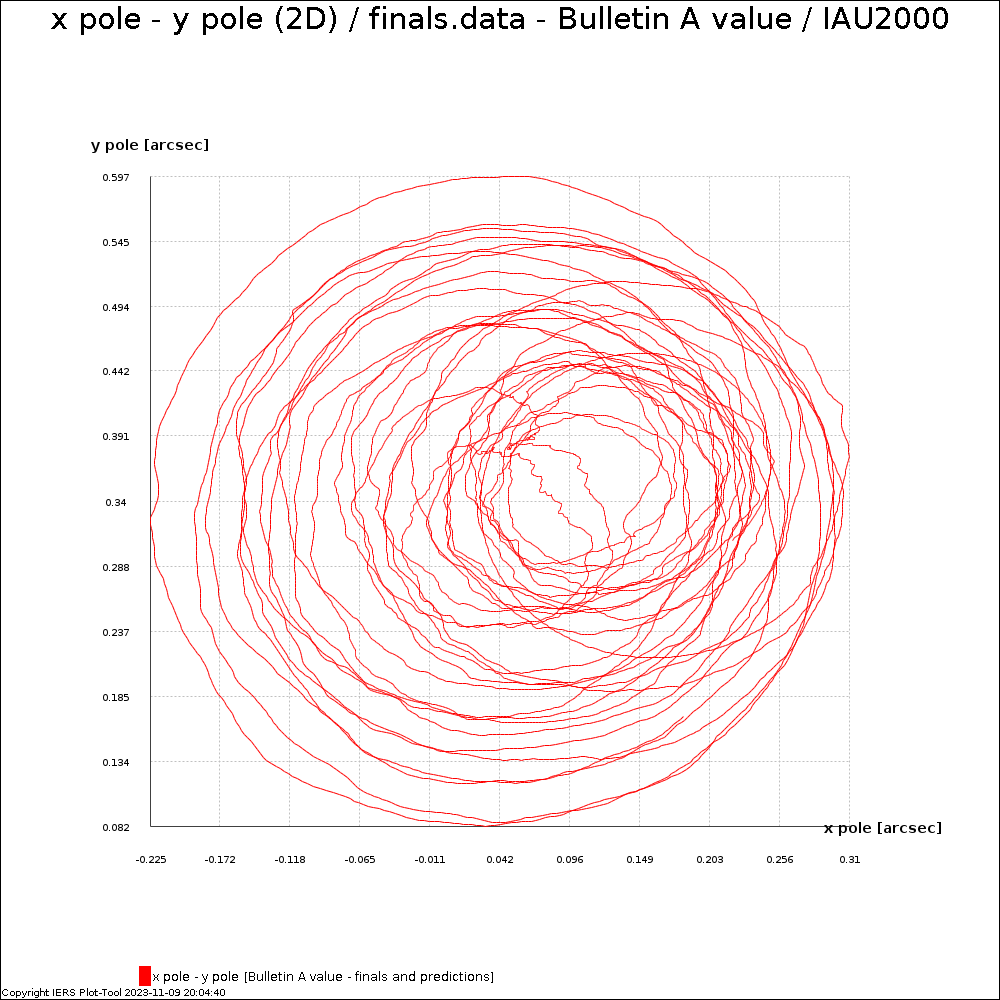
# A terrible idea would have been
# to make polar motion global.

load_polar_motion('finals2000A.all')

# Or, I could have gotten on
# the Parameter Treadmill.

data = load_file('finals2000A.all')
t = Time('utc', 2023, 11, 16, xp_yp=data)

# Instead, Skyfield code uses a ‘configuration
# object’ — a ‘Timescale’ that loads IERS data
# and serves as a factory for ‘Time’ objects:

ts = load.timescale()
t = ts.utc(2023, 11, 16)

# Thus:
#  No global settings
#  No invisible action-at-a-distance
#  No Parameter Treadmill
#  Multiple ‘Timescale’ objects can coexist

# Result? A never-ending Parameter Treadmill

def star_chart(center, targets, width_degrees=2.5,
               limiting_mag=6.5, label_fontsize=12,
               grid=False, grid_system='ecliptic',
               step_days=1.0, marker_symbol='+',
               marker_color='red', date='%m/%02d',
               output_format='png', etc=...):
    ...

Solution:
I went full LEGO

Because this isn’t about the relationship
between different parts of my library

This is about ‘foreign affairs’
with another library, matplotlib

So, instead, Skyfield’s docs
provide a full working example of
how to (a) ask Skyfield for coordinates,
then (b) go plot the star chart yourself

The user can cut-and-paste the example into their
own project, then change anything they want
•

The user can cut-and-paste the example into their
own project, then change anything they want
without having to ask me

So, whenever possible, avoid getting in the way
of a conversation between the user’s code
and another complicated library

# The philosophy of ‘getting out of the way’
# even works for simple things like I/O.
#
# It’s tempting to do the user a favor
# by creating an output file for them:

compute_data(out='table.csv')

# The user can’t skip saving to a file if
# we hard-coded that inside the function.

compute_data(out='table.csv')

# Instead, leave I/O to the user!
# Let the user go open the file:

file = open('table.csv', 'w')  # user

# Then have them pass the open file to you:

compute_data(out=file)         # your routine

A file object argument always leaves
the user free to swap in another object
that writes to a database/socket/whatever

They get full control, and
you escape the Parameter Treadmill!

Habit #3: Healthy Boundaries

Return control as soon as possible
and let the caller decide what happens next

Habits

Get off the Parameter Treadmill
Store configuration in objects
Set healthy boundaries
On a dark night, try looking at the sky

Habits

Get off the Parameter Treadmill
Store configuration in objects
Set healthy boundaries
On a dark night, try looking at the sky

Thank you! I’m @brandon_rhodes

Light-time correction	1676 Ole Rømer
Aberration
Deflection

Light-time correction	1676 Ole Rømer	40.6″
Aberration
Deflection

Width of Moon or Sun	0.5°
Naked-eye resolution	1–2′
10×50 binoculars	10″
Atmospheric blur	1–2″

Light-time correction	1676 Ole Rømer	40.6″
Aberration
Deflection

Light-time correction	1676 Ole Rømer	40.6″
Aberration	1729 James Bradley
Deflection

Precession	200 BC Hipparchus	46.8°
Nutation	1747 Bradley	18.6″
Polar motion xp,yp	1884 Chandler	0.4″